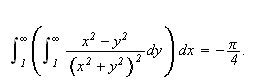
Med

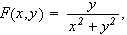 så er
så er
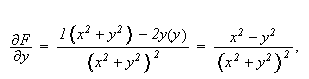
slik at integralet blir
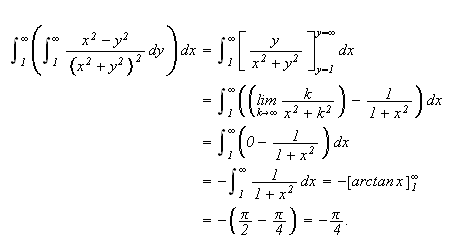
Vi skal i dette tillegget referere noen av resultatene vi trenger om uegentlige integraler i forbindelse med Fourierintegraler, nærmere bestemt i beviset for Fouriers integralteorem.
Vi fikk i forbindelse med Fourierintegralet bruk for å kunne bytte om integrasjons-rekkefølgen i dobbelt-integraler. Vi ser først på fø lgende eksempler:
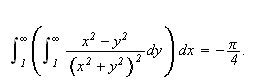
Med

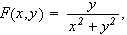 så er
så er
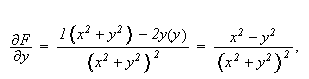
slik at integralet blir
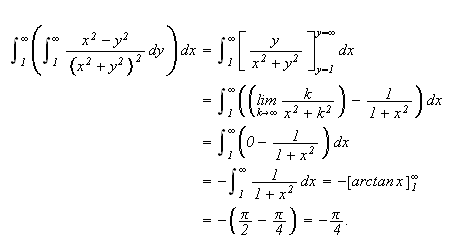
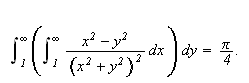
Med

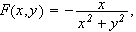 så er
så er
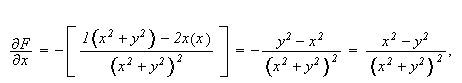
og i dette tilfellet blir integralet
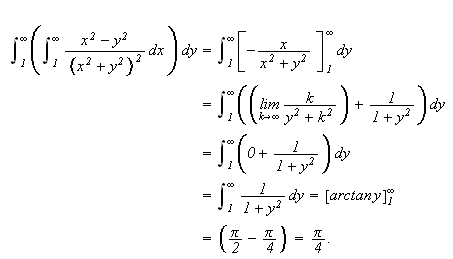
Vi får altså forskjellig svar, selv om funksjonen bare har en diskontinuitet, og denne er ikke engang inkludert i integrasjonsområdet. Som vi ser av ovenstående eksempel må vi enkelte ganger være forsiktig med å bytte om på integrasjonsrekkefølgen i itererte integraler. For endelige integrasjonsområder og kontinuerlige funksjoner kan vi bytte integrasjonsrekkefølgen fritt når integranden er kontinuerlig, men vi er altså ikke alltid garantert samme positive resultat når vi integrerer over uendelige områder.
Remediet kom først med Lebesgue (som gjorde mesteparten av arbeidet), og siden fra Fubini Note_1 og Tonelli Note_2 , som videreførte Lebesgues arbeid. Fubinis bevis var ikke komplett og Tonelli utvidet Lebesgues ideer fra begrensete funksjoner til det generelle tilfellet. Igjen er det kanskje litt urettferdig at det er Fubinis navn som gjerne henger ved dette resultatet.
[TWK, s. 229] La

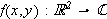 væ re kontinuerlig og la
væ re kontinuerlig og la
(i) 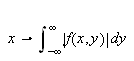
være kontinuerlig m.h.p

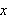 på hele
på hele

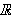 og la videre
og la videre
(ii) 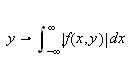
være kontinuerlig m.h.p.

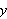 på hele
på hele

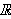 .
.
Hvis da
(iii) 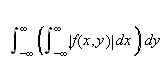
konvergerer, så vil
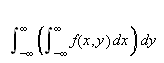
og
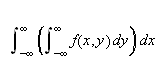
konvergere og

Beviset for Fubinis teorem kan finnes i bøker om videregående analyse, f.eks. i [B] og [TWK, s.226ff], men det er ganske omstendelig og avansert. En målteoretisk utgave av teoremet finnes i [R, s.307ff], men her forutsetter man altså generell målteori før beviset.
I lys av dette teoremet, hva gikk galt i eksemplet ovenfor? Vi skal integrere
over følgende skraverte område:
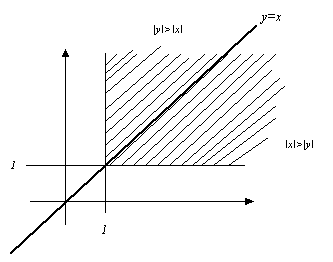
For
å få samme situasjon som i teoremet bør vi redefinere

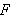 ved
ved
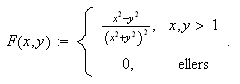
Se
på 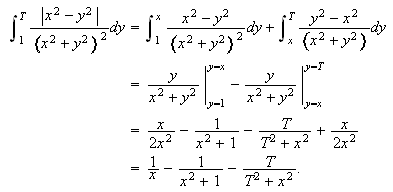
Her blir
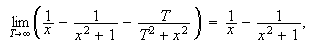
og dette gir oss da at
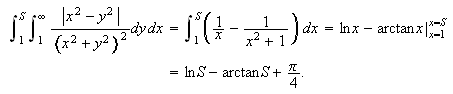
Grensen for denne er
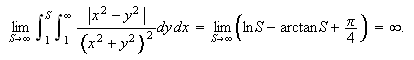
Dermed kan vi se at
integralet
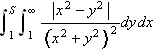 ikke konvergerer og ovenstående variant av
Fubinis teorem kan ikke brukes her.
ikke konvergerer og ovenstående variant av
Fubinis teorem kan ikke brukes her.
I beviset for Fouriers integralteorem i kapittel 6 ble det påstått at et uegentlig integral konvergerer uniformt ved Weierstrass M-test. Vi trenger først følgende definisjon:
La

 være en funksjon av to variable, f.eks.
være en funksjon av to variable, f.eks.

 .
Vi sier at
.
Vi sier at

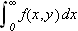 \underline{konvergerer uniformt m.h.p
\underline{konvergerer uniformt m.h.p

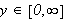 }
dersom det til hvert
}
dersom det til hvert

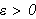 fins en
fins en

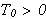 s.a. når
s.a. når

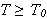 så vil
så vil
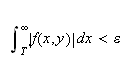
for alle

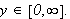
Det er litt uklart hva som egentlig er Weierstrass M-test for uegentlige
integraler. Testen blir referert til i en mengde bøker, men det er
få som nevner hvordan resultatet ser ut. Rekkevarianten er velkjent, den
sier at

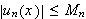 for alle
for alle

 (her er
(her er

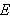 en eller annen felles definisjonsmengde for
en eller annen felles definisjonsmengde for

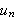 )
samt at rekken
)
samt at rekken

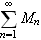 er konvergent, medfører at
er konvergent, medfører at

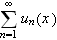 er uniformt konvergent
på
er uniformt konvergent
på 
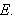 For uegentlige integraler bruker vi følgende analoge resultat:
For uegentlige integraler bruker vi følgende analoge resultat:
La

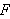 være en ikke-negativ funksjon for alle
være en ikke-negativ funksjon for alle

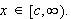 Hvis
Hvis

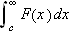 konvergerer og
konvergerer og

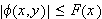 for alle
for alle

 så vil integralet
så vil integralet

konvergere uniformt
på 
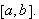
La

 være gitt. Vi vil vise at vi for alle
være gitt. Vi vil vise at vi for alle

 kan finne
kan finne

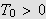 s.a.
s.a.

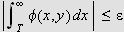 for
for

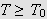 og alle
og alle

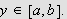 Siden
Siden

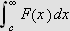 konvergerer kan vi velge
konvergerer kan vi velge

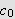 s.a.
s.a.

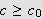 medfører
medfører
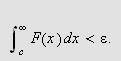
Pr. antagelse har vi da for alle

 at:
at:

Altså konvergerer

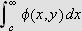 uniformt
m.h.p.
uniformt
m.h.p. 
 .
.
La oss se en gang til på situasjonen i beviset for Fouriers
integralteorem. I beviset har vi

 og
og

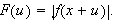 Her er
Her er

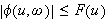 og substitusjonen som er brukt i beviset,
og substitusjonen som er brukt i beviset,

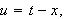 gir videre at
gir videre at

siden

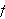 er antatt absolutt integrerbar i teoremet. Altså vil
er antatt absolutt integrerbar i teoremet. Altså vil

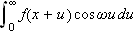 konvergere uniformt for
konvergere uniformt for

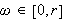 ved
ved

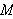 -testen.
-testen.
Når integranden er kontinuerlig (eller stykkevis kontinuerlig) m.h.p.

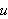 og
og

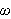 har vi opplagt at
har vi opplagt at
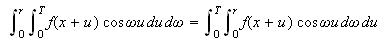
når integrasjonsområdet er endelig. Det vi trenger i beviset er
å vite hva som skjer når

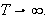 Til en gitt
Til en gitt

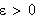 finner vi derfor en
finner vi derfor en

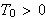 s.a.
s.a.

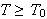 medfører at
medfører at
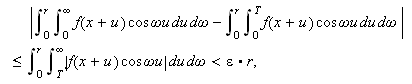
siden det innerste integralet konvergerer uniformt for

 .
På grunn av () har vi da at
.
På grunn av () har vi da at
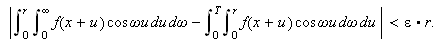
Men dette holder jo for alle

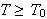 og dermed vet vi at
og dermed vet vi at
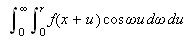
eksisterer med samme verdi som
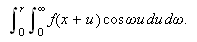
| \lbrack R] | Royden, H.L: Real Analysis |
| Prentice Hall, Inc (1988); ISBN: 0-02-404151-3 | |
| \lbrack B] | Buck, R.C.: Advanced Calculus
3  ed.
ed. |
| The McGraw Hill Companies, New York (1978); ISBN: 0070087288 | |
| \lbrack TWK] | Körner, T.W.: Fourier Analysis |
| Cambridge university press (1988); ISBN: 0-521-25120-6 | |
| \lbrack B/C] | Brown, Churchill: Fourier series and boundary value
problems, 6
  ed.
ed. |
| McGraw-Hill Higher education (2001); ISBN: 0071181512 |
Neste: Gibbs fenomen