
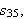 den 35'te partialsummen i Fourierrekka, og får følgende graf:
den 35'te partialsummen i Fourierrekka, og får følgende graf:
Vi har brukt en del tid på å vise hvordan Fourier-rekker konvergerer. Nå er det på tide å vise at de ikke konvergerer så bra i alle tenkelige situasjoner. La oss se på Gibbs' fenomen Note_1 som er betegnende for hva som skjer med Fourierrekker nær diskontinuiteter.
Michelson konstruerte en maskin som kunne finne en funksjon ut fra dens
Fourierkoeffisienter. Etter å matet 80 koeffisienter inn i maskinen
forventet Michelson å få ut en sagblad-funksjon, men fikk en utgave
med to små ''hatter'' nær diskontinuitetspunktene. Denne egenskapen
er kanskje enda lettere å observere når vi ser på Fourierrekka
vi diskuterte i kapittel 1. Vi plotter

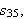 den 35'te partialsummen i Fourierrekka, og får følgende graf:
den 35'te partialsummen i Fourierrekka, og får følgende graf:
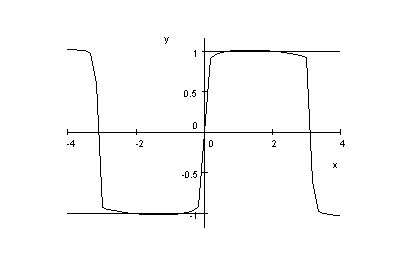
Illustrasjon av Gibbs'
fenomen
Michelson var kjent som ekstremt dyktig med slike maskiner,
men bare beregninger for hånd fikk overbevist ham om at slike hatter
faktisk eksisterte i partialsummen for en Fourierrekke. Man skulle tro at
disse hattene forsvinner etter hvert som man beregner flere og flere ledd (og
det trodde nok Michelson også), siden alt ser ut til å konvergere.
Men uansett hvor mange ledd Michelson beregnet, var fortsatt den totale feilen
(altså feilen over funksjonen for

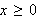 og feilen under funksjonen for
og feilen under funksjonen for

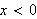 ) på 17-18%
, men hattene nærmet seg iallfall diskontinuitetspunktet.
) på 17-18%
, men hattene nærmet seg iallfall diskontinuitetspunktet.
Problemet ble omtalt av Gibbs i to brev han skrev til Nature
i 1899. Hatten like til høyre for 0 er
litt høyere enn grensen til funksjonen når vi nærmer oss

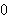 fra høyre. Verdien vi skulle ønske rekka hadde er
fra høyre. Verdien vi skulle ønske rekka hadde er

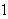 ,
men den ser ut til å være nærmere
,
men den ser ut til å være nærmere

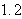 .
Det samme fenomenet inntreffer på undersiden av grafen når vi
nærmer oss
.
Det samme fenomenet inntreffer på undersiden av grafen når vi
nærmer oss

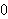 fra venstre. Selv om vi hadde plottet mange flere ledd i partialsummen, hadde
ikke disse sup- og inf-verdiene til partialsummen ligget noe nærmere
grafen. Dette til tross for at vi har punktvis konvergens
på
fra venstre. Selv om vi hadde plottet mange flere ledd i partialsummen, hadde
ikke disse sup- og inf-verdiene til partialsummen ligget noe nærmere
grafen. Dette til tross for at vi har punktvis konvergens
på 
![$[-\pi ,\pi ].$](gibbs__9.png) Slik er dette også en god demonstrasjon på forskjellen mellom
uniform og punktvis konvergens. Slike fenomener inntrer ikke ved uniform
konvergens. En snodig detalj oppi det hele. Igjen er
det kanskje feil mann som har fått navnet sitt hengende ved begrepet.
Henry Wilbraham hadde nemlig gjordt de samme observasjoner over 50 år
tidligere. I tillegg kom litt senere (1906) Maxime Bôcher mye lenger i
sine analyser, nemlig ved å vise at en feil på 9% er en generell
egenskap ved Fourierrekker nær diskontinuitetspunkter. Så Gibbs kom
ikke først med resultatet, ga ikke ut noe bevis og begrenset seg til et
spesialtilfelle. Likevel kalles dette i dag Gibbs' fenomen.
Slik er dette også en god demonstrasjon på forskjellen mellom
uniform og punktvis konvergens. Slike fenomener inntrer ikke ved uniform
konvergens. En snodig detalj oppi det hele. Igjen er
det kanskje feil mann som har fått navnet sitt hengende ved begrepet.
Henry Wilbraham hadde nemlig gjordt de samme observasjoner over 50 år
tidligere. I tillegg kom litt senere (1906) Maxime Bôcher mye lenger i
sine analyser, nemlig ved å vise at en feil på 9% er en generell
egenskap ved Fourierrekker nær diskontinuitetspunkter. Så Gibbs kom
ikke først med resultatet, ga ikke ut noe bevis og begrenset seg til et
spesialtilfelle. Likevel kalles dette i dag Gibbs' fenomen.
Som et eksempel [B/N/B, s.481f] ser vi på funksjonen
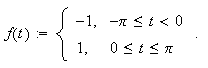
Vi skal vise at feilen til partialsummen er ca. 9% av størrelsen til
diskontinuiteten, både over og under grafen til denne funksjonen. Vi
regner først ut Fourierrekka til

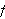 .
Vi merker oss at
.
Vi merker oss at

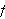 er en odde funksjon, og dermed er
er en odde funksjon, og dermed er

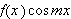 også odde, slik at
også odde, slik at

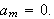
Vi finner også
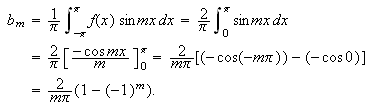
Altså er
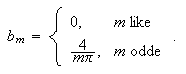
Vi setter derfor

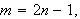 slik at
slik at

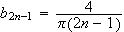 for
for

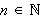 .
Fourierrekka blir da
.
Fourierrekka blir da
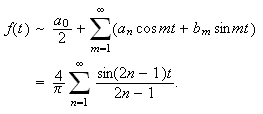
Vi vet nå, etter Dirichlets bevis, at denne konvergerer punktvis mot

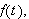 bortsett fra der vi har diskontinuitetspunkter. Det har vi i
bortsett fra der vi har diskontinuitetspunkter. Det har vi i

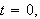 og det er rundt dette punktet vi skal observere Gibbs' fenomen. Vi lar
og det er rundt dette punktet vi skal observere Gibbs' fenomen. Vi lar

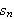 betegne
betegne

 'te
partialsum til Fourierrekka,
'te
partialsum til Fourierrekka,
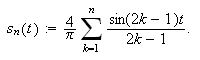
Vi bruker som vanlig derivasjon for å undersøke ekstremalverdier.
Derivasjon av partialsummen gir
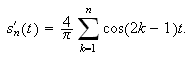
Vi ser først at
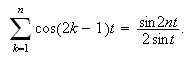
Anta


 .
Multilpliser så rekka med
.
Multilpliser så rekka med

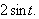 Igjen trenger vi den trigonometriske identiteten
Igjen trenger vi den trigonometriske identiteten
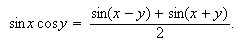
Vi får da
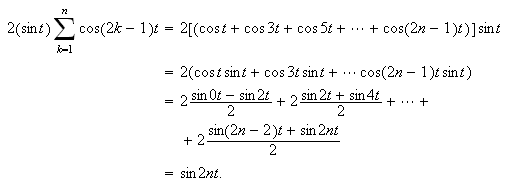
Altså er
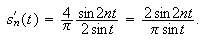
Kritiske punkt for

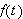 er da
er da

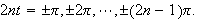 Det gir at de nærmeste kritiske punkt ligger
på
Det gir at de nærmeste kritiske punkt ligger
på 
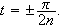 Nå har
Nå har

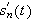 fast fortegn nær
fast fortegn nær

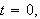 så vi ser vi har topp for
så vi ser vi har topp for

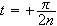 og bunn for
og bunn for

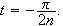 Vi konsentrer oss om høyresiden av
Vi konsentrer oss om høyresiden av

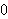 ,
da venstre side har tilsvarende argument. Plasseringen til disse toppene vil
nærme seg
,
da venstre side har tilsvarende argument. Plasseringen til disse toppene vil
nærme seg

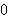 både fra høyre og venstre hver for seg når
både fra høyre og venstre hver for seg når

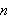 går mot uendelig. Ved å sette inn for
går mot uendelig. Ved å sette inn for

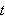 finner vi
finner vi

Den siste summen er en Riemann-sum for

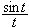 på intervallet
på intervallet

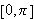 med maskevidde
med maskevidde

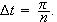 Når
Når

 vil derfor denne summen konvergere mot Riemann-integralet
vil derfor denne summen konvergere mot Riemann-integralet
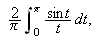
slik at
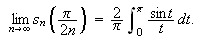
Dette er et kjent integral og verdien finnes i tabeller. Denne verdien er
omlag

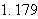 .
Vi kan tilnærme verdien ved Taylorpolynomet til
.
Vi kan tilnærme verdien ved Taylorpolynomet til

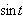 nær 0,
nær 0,
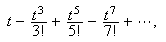
som gir
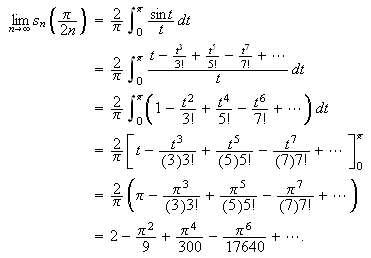
En tilnærmelse med to desimaler her blir 1.18. Derfor har vi

altså er verdien til partialsummen når vi nærmer oss 0 fra
høyre omtrent 9% større enn størrelsen
på diskontinuiteten. Generelt kan vi si
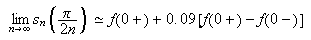
og
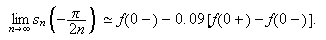
| \lbrack B/N/B] | Bachman, G./Narici, L./Beckenstein, E.: Fourier and Wavelet analysis |
| Springer Verlag New York 2000. ISBN: 0-387-98899-8 | |
| \lbrack TWK] | Körner, T.W.: Fourier analysis |
| Cambridge university press (1988); ISBN: 0-521-25120-6 |